Managing 32-bit floating point precision with relative camera offsets

Filament vertex shaders expose the getWorldFromModelMatrix() function, which is used to compute the position of the vertex in 'world space':

void materialVertex(inout MaterialVertexInputs material) {
    vec3 position = getPosition().xyz;
    material.worldPosition.xyz = (getWorldFromModelMatrix() * vec4(position, 1.0f)).xyz;
}

If your material uses vertexDomain: object, you don't need to explicitly compute this value; this has already been computed internally before materialVertex() is invoked (see initMaterialVertex in surface_material_inputs.vs and computeWorldPosition in surface_getters.vs).

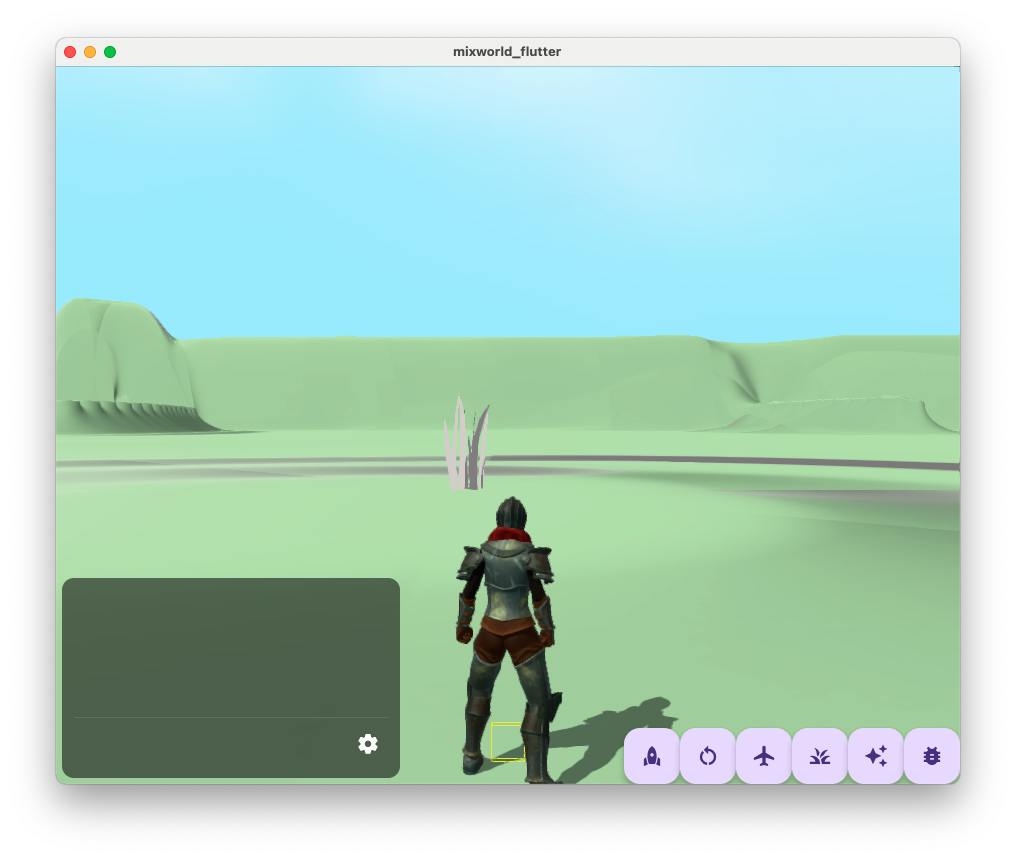
With an identity transform, the tuft of grass is rendered at (0,0,0) in world space, as we'd expect

Since this matrix transforms the position of each vertex from model space to 'world space', this is conceptually similar to the model matrix. However, there's one important qualification in the Filament documentation:

“world space” in Filament's shading system does not necessarily match the API-level world space. To obtain the position of the API-level camera, custom materials can use getUserWorldFromWorldMatrix() to transform getWorldCameraPosition().

This suggests that the 'world space' position computed from getWorldFromModelMatrix is not the 'real' world space position of the vertex. We can verify this by omitting the world transform when setting 'material.worldPosition':

void materialVertex(inout MaterialVertexInputs material) {
    vec3 position = getPosition().xyz;
    material.worldPosition.xyz = position;
}

If material.worldPosition was the 'real' world space position for the vertex, we would expect to see the tuft of grass rendered at the same position as above. That's not the case:

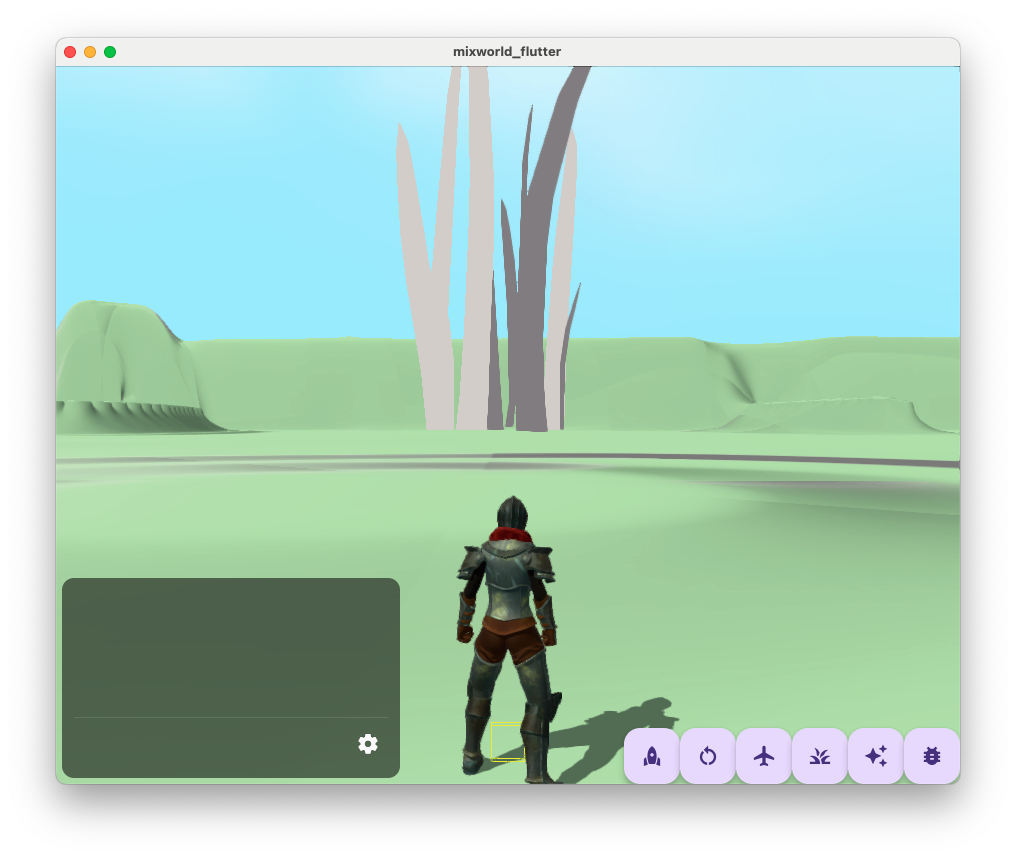
We see something quite different; in fact, the tuft of grass actually moves with the camera:

This suggests that material.worldPosition and getWorldFromModelMatrix() are actually relative to the camera position rather than the true world position.

Let's check the Filament source to see what's going on. getWorldFromModelMatrix returns the value of the uniform object_uniforms_worldFromModelMatrix, which has been set to the value of sceneData.elementAt<WORLD_TRANSFORM>() in FScene::prepareVisibleRenderables. This latter value itself is shaderWorldTransform in FScene::prepare:

const mat4f shaderWorldTransform{
        worldTransform * tcm.getWorldTransformAccurate(ti) };

getWorldTransformAccurate() returns the 'real' world transform for the renderable instance. worldTransform was passed from FRenderer::renderJob to FView::prepare and FScene::prepare, and is actually computed in FView::computeCameraInfo:

CameraInfo FView::computeCameraInfo(FEngine& engine) const noexcept {
    double3 translation;
    FCamera const* const camera = mViewingCamera ? mViewingCamera : mCullingCamera;
    if (engine.debug.view.camera_at_origin) {
        // this moves the camera to the origin, effectively doing all shader computations in
        // view-space, which improves floating point precision in the shader by staying around
        // zero, where fp precision is highest. This also ensures that when the camera is placed
        // very far from the origin, objects are still rendered and lit properly.
        translation = -camera->getPosition();
    }
    return { *camera, mat4{ rotation } * mat4::translation(translation) };
}

So when camera_at_origin is true (the default), worldTransform is actually the negative of the camera position. Multiplying the vertex position by getWorldFromModelMatrix() in the vertex shader actually returns the position of the vertex relative to the camera. Or, to think of it another way, the world origin is moved to the camera origin before any vertex or fragment calculations take place.

Per the documentation, we can recover the "true" world space position of the camera by multiplying getWorldCameraPosition() by getUserWorldFromWorldMatrix(). From src/ds/ColorPassDescriptorSet.cpp, we see this latter value is simply the inverse of the camera world transform calculated in computeCameraInfo above:

s.userWorldFromWorldMatrix = mat4f(inverse(camera.worldTransform));

So the matrix returned by getWorldFromModelMatrix() translates the vertex to the position of the camera, and getUserWorldFromWorldMatrix moves it back. Filament's "world space" is therefore what we refer to above as "camera offset space", and Filament's "API-level world space" is what I refer to as "true worldspace".

The reason for this is floating point precision.

32-bit floating point numbers

A 32-bit number ranges from 0000 0000 0000 0000 0000 0000 0000 0000 and 00 00 00 00 to 1111 1111 1111 1111 1111 1111 1111 1111 and FF FF FF FF in binary and hexadecimal respectively.

If this represents an IEEE 754 floating point number, the smallest (negative) and largest (positive) finite values will be:

1. 1111 1111 0111 1111 1111 1111 1111 1111, FF 7F FF FF and -3.40282346638528859811704E+38
2. 0111 1111 0111 1111 1111 1111 1111 1111, 7F 7F FF FF and 3.402823466385288598117042E+38

in binary, hexadecimal and scientific decimal notation respectively (or in C, -FLT_MAX and FLT_MAX). All-zeros/all-ones aren't used for FLT_MIN/FLT_MAX because some bits are reserved for infinity, signed zeros, etc.

Consider a camera positioned at (FLT_MAX, 0.0, 0.0). By decrementing the last bit of FLT_MAX (i.e. 7F 7F FF FE), we will find the closest 32-bit floating point number to FLT_MAX in the direction of the origin. This equates to 3.402823263561192561600338E+38 in decimal, roughly 2e31 world units away from FLT_MAX! Clearly, there is a huge loss of precision when working with large floats.

Let's look at the following triangle:

            (0,0.5,0)
               /\
              /  \
(-0.5,0.0,0) /____\ (0.5,0.0,0)

Imagine we want to translate this triangle by (10_000_000, 0, 0) (or 4B 18 96 80 in hex float 32). We would expect the vertices to be positioned like so:

                (10_000_000,0.5,0)
                      /\
                     /  \
(9_999_999.5,0.0,0) /____\ (10_000_000.5,0.0,0)

However, neither 9_999_999.5 nor 10_000_000.5 can be exactly represented as a 32-bit floating point number. In hexadecimal, the closest 32-bit floating point numbers will be at either (9_999_999, 0, 0)/4B 18 96 7F in the negative direction or (10_000_001, 0, 0)/4B 18 96 81 (in the positive direction). Applying this transform will most likely round both values to 10_000_000, collapsing the triangle to a single point. We can verify this with numpy:

>>> import numpy
>>> numpy.float32(10_000_000) + numpy.float32(0.5)
10000000.0
>>> numpy.float32(10_000_000) + numpy.float32(-0.5)
10000000.0

Python's float is almost always a 64-bit floating point number, so I'm using numpy to make sure I'm working with 32-bit floats.

Since floating point numbers have greater precision the closer you get to zero, if we're forced to work with only 32-bits, we can squeeze more precision by reducing the absolute size of the value it contains.

For example, we could adjust the model matrix so that all transforms are specified relative to the camera position, rather than the world origin.

Imagine a camera positioned at (9_999_990, 0, 0), looking at our triangle above. In "camera offset space", the transformed triangle origin is at (10,0,0) (rather than (10_000_000, 0, 0) in "real world space"). This leaves us with sufficient precision to render the triangle above:

>>> numpy.float32(10) + numpy.float32(0.5)
10.5
>>> numpy.float32(10) + numpy.float32(-0.5)
9.5

Returning to Filament, it should be clear that moving the world origin to the camera origin is Filament's way to maximize precision for floating point calculations.